Materi Matematika Histogram Memahami Distribusi Data

Berita Terkait

Materi matematika histogram memberikan gambaran visual yang efektif tentang distribusi data numerik. Dengan memahami konsep dasar dan cara membuat histogram, kita dapat dengan mudah menganalisis pola dan tren dalam data, serta membandingkan berbagai kelompok data.

Artikel ini akan membahas secara menyeluruh mengenai histogram, mulai dari definisi, komponen, cara pembuatan, interpretasi, hingga contoh penerapannya dalam matematika. Kita juga akan melihat perbedaan histogram dengan jenis grafik lainnya, serta potensi permasalahan dan solusinya.

Definisi Histogram

Histogram adalah representasi visual dari distribusi frekuensi data numerik. Dengan menampilkan data dalam bentuk batang yang berdampingan, histogram memudahkan pemahaman pola dan tren dalam data. Informasi ini sangat penting untuk analisis data dan pengambilan keputusan.

Definisi Histogram

Histogram merupakan grafik batang yang digunakan untuk menampilkan distribusi frekuensi data numerik. Setiap batang merepresentasikan rentang nilai data tertentu, dan tinggi batang menunjukkan frekuensi data yang berada dalam rentang tersebut. Konsep dasar histogram terletak pada pengelompokan data ke dalam interval atau kelas yang berurutan dan berkesinambungan.

Konsep Dasar dalam Distribusi Frekuensi

Histogram erat kaitannya dengan distribusi frekuensi. Data dikelompokkan ke dalam kelas-kelas yang saling tidak tumpang tindih. Tinggi setiap batang pada histogram menunjukkan banyaknya data yang jatuh ke dalam kelas tersebut. Rentang nilai data pada setiap kelas sama lebarnya.

Ilustrasi Sederhana

Misalnya, terdapat data nilai ujian matematika dari 20 siswa: 70, 75, 80, 85, 90, 72, 78, 82, 88, 92, 75, 80, 85, 90, 95, 78, 83, 88, 93, 98. Data ini dapat dikelompokkan ke dalam kelas-kelas seperti 70-79, 80-89, 90-99. Histogram akan menampilkan tinggi masing-masing batang berdasarkan jumlah siswa yang mendapat nilai di rentang kelas tersebut. Semakin tinggi batang, semakin banyak siswa yang mendapat nilai dalam rentang kelas tersebut.

Jenis-jenis Histogram dan Karakteristiknya

Beberapa jenis histogram yang umum digunakan antara lain:

Histogram Simetris: Bentuk histogram simetris menunjukkan distribusi data yang terpusat di sekitar nilai tengah. Data terdistribusi merata di kedua sisi.
Histogram Miring Kanan (Positif): Histogram miring ke kanan menunjukkan bahwa sebagian besar data terkonsentrasi di sisi kiri histogram, dan ekornya memanjang ke kanan. Nilai-nilai ekstrim pada sisi kanan cenderung lebih besar.
Histogram Miring Kiri (Negatif): Histogram miring ke kiri menunjukkan bahwa sebagian besar data terkonsentrasi di sisi kanan histogram, dan ekornya memanjang ke kiri. Nilai-nilai ekstrim pada sisi kiri cenderung lebih besar.

Penggunaan Histogram untuk Data Numerik

Histogram digunakan untuk menggambarkan distribusi frekuensi data numerik. Dengan melihat bentuk histogram, kita dapat memperoleh gambaran umum tentang bagaimana data tersebar. Histogram dapat digunakan untuk mengidentifikasi pusat data, sebaran, dan adanya outlier. Informasi ini sangat bermanfaat untuk analisis data lebih lanjut, seperti perhitungan rata-rata, median, dan standar deviasi.

Komponen Histogram: Materi Matematika Histogram

Histogram merupakan visualisasi data yang efektif untuk melihat distribusi frekuensi. Memahami komponen-komponennya sangat penting untuk menginterpretasikan informasi yang terkandung di dalamnya.

Komponen-Komponen Penting

Histogram terdiri dari beberapa komponen yang saling berkaitan. Masing-masing komponen memiliki peran penting dalam menggambarkan data.

Sumbu Horizontal (Sumbu X): Sumbu ini menunjukkan rentang nilai data. Rentang nilai tersebut dibagi menjadi beberapa interval atau kelas. Interval-interval ini mewakili kelompok data yang serupa. Interval ini penting untuk mengelompokkan data.
Sumbu Vertikal (Sumbu Y): Sumbu ini menunjukkan frekuensi atau jumlah data yang masuk ke dalam setiap interval pada sumbu X. Semakin tinggi batang histogram di suatu interval, semakin banyak data yang berada di interval tersebut.
Batang-Batang Histogram: Batang-batang ini merepresentasikan frekuensi data dalam setiap interval. Tinggi batang menunjukkan banyaknya data yang masuk ke dalam interval tertentu. Setiap batang berdampingan tanpa celah, menunjukan hubungan kontinu antara interval.
Judul Grafik: Judul grafik menjelaskan topik data yang ditampilkan. Judul yang jelas dan informatif memudahkan pembaca untuk memahami maksud histogram.
Label Sumbu: Label pada sumbu X dan Y menjelaskan satuan atau variabel yang diukur. Label ini sangat penting untuk interpretasi data yang akurat.

Tabel Komponen Histogram

Komponen	Fungsi
Sumbu Horizontal (X)	Menunjukkan rentang nilai data, dibagi menjadi interval.
Sumbu Vertikal (Y)	Menunjukkan frekuensi data dalam setiap interval.
Batang-Batang Histogram	Merepresentasikan frekuensi data dalam interval tertentu.
Judul Grafik	Memberikan gambaran singkat tentang topik data.
Label Sumbu	Menjelaskan satuan atau variabel yang diukur pada masing-masing sumbu.

Hubungan Antar Komponen

Semua komponen dalam histogram saling terkait dan bergantung satu sama lain. Sumbu X dan Y menentukan skala dan rentang data yang ditampilkan. Batang-batang histogram bergantung pada frekuensi data di setiap interval pada sumbu X. Judul dan label sumbu memberikan konteks yang diperlukan untuk menginterpretasikan data.

Contoh Histogram

Bayangkan kita ingin melihat distribusi tinggi badan siswa di suatu kelas. Berikut contoh histogram sederhana:

Judul: Distribusi Tinggi Badan Siswa Kelas X

Sumbu X: Tinggi badan (cm), dibagi interval 150-155, 155-160, 160-165, 165-170, 170-175.

Sumbu Y: Frekuensi (banyaknya siswa).

Batang-batang Histogram: Tinggi batang menunjukkan banyak siswa dengan tinggi badan di dalam interval tersebut. Misalnya, batang untuk interval 160-165 cm mungkin lebih tinggi dari batang lainnya, menunjukan lebih banyak siswa memiliki tinggi badan di rentang tersebut.

Label Sumbu: Sumbu X diberi label “Tinggi Badan (cm)” dan sumbu Y diberi label “Frekuensi (Siswa)”.

Catatan: Contoh histogram di atas merupakan ilustrasi. Data dan angka-angka spesifik mungkin berbeda tergantung pada data yang dianalisis.

Cara Membuat Histogram

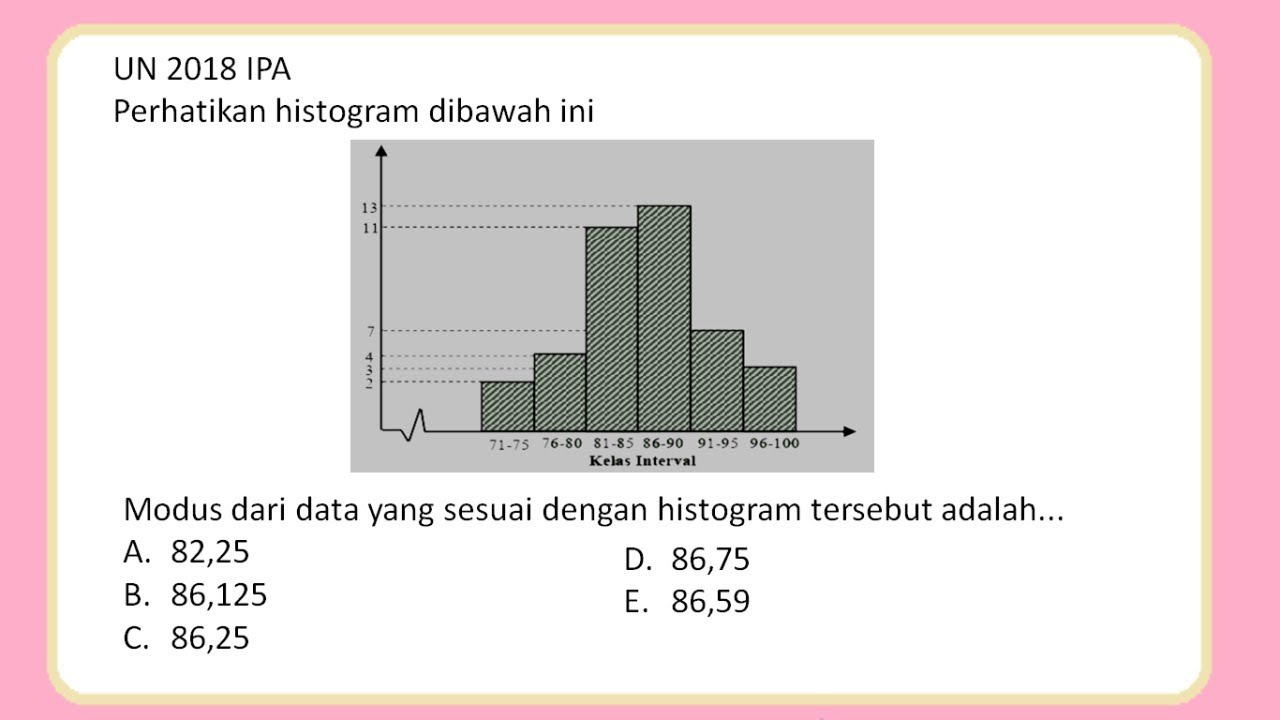
Histogram merupakan visualisasi data yang sangat berguna untuk melihat distribusi frekuensi suatu variabel. Pemahaman tentang cara membuat histogram akan membantu kita menganalisis data dengan lebih baik. Dalam pembahasan ini, akan dijelaskan langkah-langkah praktis untuk membuat histogram, termasuk bagaimana menghitung frekuensi dan membagi data ke dalam interval yang sesuai.

Langkah-langkah Pembuatan Histogram

Berikut langkah-langkah yang perlu diikuti untuk membuat histogram:

Mengidentifikasi Rentang Data: Tentukan nilai minimum dan maksimum dari data yang akan divisualisasikan. Rentang data ini akan menjadi dasar untuk menentukan interval.
Menentukan Banyaknya Interval: Tentukan jumlah interval yang akan digunakan. Jumlah interval yang tepat bergantung pada jumlah data dan rentangnya. Interval yang terlalu banyak atau terlalu sedikit dapat menyulitkan interpretasi data. Sebagai panduan umum, jumlah interval bisa antara 5 hingga 20.
Menentukan Lebar Interval: Hitung lebar setiap interval dengan membagi rentang data dengan jumlah interval. Pastikan lebar interval konsisten untuk semua interval.
Membagi Data ke dalam Interval: Tempatkan setiap nilai data ke dalam interval yang sesuai berdasarkan batas-batas interval yang telah ditentukan.
Menghitung Frekuensi: Hitung berapa banyak data yang masuk ke dalam setiap interval. Frekuensi ini akan menjadi tinggi batang pada histogram.
Membuat Grafik: Gambar sumbu horizontal (sumbu x) untuk mewakili interval dan sumbu vertikal (sumbu y) untuk mewakili frekuensi. Buat batang untuk setiap interval dengan tinggi yang sesuai dengan frekuensinya. Batang-batang ini saling berdekatan, tanpa spasi di antara mereka.

Contoh Pembuatan Histogram

Misalkan kita memiliki data nilai ujian matematika 10 siswa:

70, 75, 80, 85, 90, 90, 95, 95, 95, 100

Langkah-langkahnya:

Rentang data: Nilai minimum 70, maksimum 100.
Banyaknya interval: Kita pilih 5 interval.
Lebar interval: (100 – 70) / 5 = 6
Interval: 70-75, 76-81, 82-87, 88-93, 94-99, 100
Frekuensi:
- 70-75: 1
- 76-81: 0
- 82-87: 0
- 88-93: 2
- 94-99: 3
- 100: 1
Histogram: Histogram akan memiliki batang dengan tinggi yang merepresentasikan frekuensi setiap interval.

Diagram Alur Pembuatan Histogram

Berikut diagram alur sederhana yang menggambarkan proses pembuatan histogram:

(Diagram alur tidak dapat ditampilkan dalam teks. Diagram alur akan menunjukkan urutan langkah-langkah di atas dalam bentuk kotak-kotak yang terhubung dengan panah. Diagram akan menunjukkan proses mulai dari identifikasi rentang data sampai pembuatan histogram.)

Interpretasi Histogram

Histogram merupakan alat visualisasi yang sangat berguna untuk memahami distribusi data. Dengan melihat bentuk histogram, kita dapat mengidentifikasi pola dan tren dalam data, serta membandingkan karakteristik antar kelompok data. Pemahaman yang baik tentang interpretasi histogram akan membantu dalam pengambilan keputusan yang lebih terinformasi berdasarkan data yang disajikan.

Memahami Pola Distribusi Data

Bentuk histogram memberikan gambaran umum mengenai distribusi data. Histogram yang menumpuk di bagian tengah menunjukkan data cenderung terpusat di sekitar nilai tertentu, sedangkan histogram yang memanjang ke kiri atau kanan mengindikasikan data yang cenderung miring atau tidak simetris.

Distribusi Normal (Normal Distribution): Histogram berbentuk lonceng simetris dengan puncak di tengah. Hal ini mengindikasikan data terdistribusi merata di sekitar rata-rata.
Distribusi Miring Kanan (Positively Skewed): Histogram memiliki ekor yang panjang di sebelah kanan, menunjukkan data cenderung memiliki beberapa nilai yang lebih besar dari rata-rata.
Distribusi Miring Kiri (Negatively Skewed): Histogram memiliki ekor yang panjang di sebelah kiri, menunjukkan data cenderung memiliki beberapa nilai yang lebih kecil dari rata-rata.
Distribusi Multimodal: Histogram memiliki lebih dari satu puncak, mengindikasikan adanya lebih dari satu kelompok data yang terpisah.

Identifikasi Tren dan Pola

Selain bentuk umum, kita juga dapat mengidentifikasi tren dan pola lain dari histogram. Perubahan frekuensi pada rentang nilai tertentu dapat mengindikasikan kecenderungan tertentu dalam data.

Perubahan Frekuensi: Perhatikan perubahan frekuensi pada kelas-kelas tertentu. Apakah ada peningkatan atau penurunan frekuensi secara berurutan? Hal ini dapat mengindikasikan tren dalam data.
Kelompok Data yang Berbeda: Perhatikan apakah ada perbedaan yang mencolok dalam distribusi data antar kelompok. Hal ini bisa membantu membandingkan karakteristik antar kelompok.

Membandingkan Dua atau Lebih Kelompok Data

Histogram dapat digunakan untuk membandingkan dua atau lebih kelompok data. Dengan membandingkan bentuk dan distribusi histogram dari masing-masing kelompok, kita dapat melihat perbedaan dan kesamaan karakteristik antar kelompok tersebut.

Kelompok Data A	Kelompok Data B
Histogram menunjukkan distribusi data yang terpusat di sekitar nilai 50.	Histogram menunjukkan distribusi data yang terpusat di sekitar nilai 70.

Contoh Interpretasi

Misalkan kita ingin menganalisis waktu yang dibutuhkan mahasiswa untuk menyelesaikan tugas akhir. Histogram dari data waktu penyelesaian tugas akhir dapat menunjukkan pola distribusi data. Jika histogram menunjukkan distribusi yang miring ke kanan, hal ini mengindikasikan bahwa ada beberapa mahasiswa yang membutuhkan waktu lebih lama untuk menyelesaikan tugas akhir, dibandingkan dengan mahasiswa lainnya.

Contoh Penerapan Histogram dalam Matematika

Histogram merupakan alat visualisasi data yang efektif dalam matematika. Dengan menyajikan data dalam bentuk grafik batang, histogram memudahkan kita untuk memahami distribusi data dan mengidentifikasi pola-pola penting. Pemahaman ini sangat krusial dalam berbagai aplikasi, termasuk analisis statistik dan pengambilan keputusan.

Penerapan dalam Analisis Data

Histogram dapat digunakan untuk menganalisis data dalam berbagai konteks matematika. Misalnya, dalam mempelajari distribusi nilai ujian siswa, histogram dapat menunjukkan sebaran nilai-nilai tersebut. Hal ini memungkinkan guru untuk mengidentifikasi rentang nilai yang paling sering muncul dan juga nilai-nilai ekstrem.

Dalam penelitian ilmiah, histogram dapat membantu mengidentifikasi distribusi frekuensi suatu variabel, misalnya distribusi tinggi badan populasi.
Histogram juga bermanfaat dalam analisis data ekonomi, seperti distribusi pendapatan penduduk atau distribusi harga suatu produk.
Dalam industri, histogram dapat digunakan untuk menganalisis kualitas produk, misalnya distribusi ukuran produk atau distribusi waktu produksi.

Pengambilan Keputusan Berbasis Data

Informasi yang disajikan dalam histogram dapat menjadi landasan bagi pengambilan keputusan. Dengan melihat pola dan distribusi data, kita dapat membuat prediksi, mengambil tindakan, atau mengembangkan strategi yang lebih baik. Contohnya, dalam bisnis, histogram dapat membantu dalam menentukan strategi pemasaran yang tepat.

Histogram dapat memberikan gambaran yang jelas mengenai sebaran data, membantu dalam mengidentifikasi tren dan pola.
Dengan melihat distribusi frekuensi, kita dapat menentukan apakah data terdistribusi normal atau tidak.
Histogram dapat membantu dalam membandingkan distribusi data dari beberapa kelompok atau sampel.

Contoh Kasus

Bayangkan sebuah sekolah ingin menganalisis hasil ujian matematika kelas 10. Mereka mengumpulkan nilai ujian 50 siswa. Histogram dapat digunakan untuk menggambarkan distribusi nilai-nilai tersebut. Dari histogram, sekolah dapat melihat rentang nilai yang paling banyak didapatkan siswa (misalnya, rentang 70-80) dan juga seberapa banyak siswa yang mendapatkan nilai di bawah atau di atas rata-rata.

Rentang Nilai	Frekuensi
60-70	5
70-80	20
80-90	15
90-100	10

Dari tabel di atas, dapat dilihat bahwa sebagian besar siswa mendapatkan nilai di rentang 70-80. Sekolah dapat menggunakan informasi ini untuk merencanakan program remedial atau pengayaan bagi siswa yang membutuhkan.

Ilustrasi Penyebaran Data, Materi matematika histogram

Histogram dapat menggambarkan penyebaran data secara visual. Jika data terkonsentrasi pada satu rentang nilai, histogram akan menunjukkan puncak yang tinggi pada rentang tersebut. Sebaliknya, jika data tersebar merata, histogram akan menunjukkan puncak yang rendah dan merata di seluruh rentang nilai.

Misalnya, dalam sebuah histogram tentang tinggi badan siswa, jika puncak berada di rentang 160-170 cm, berarti sebagian besar siswa memiliki tinggi badan di kisaran tersebut. Sebaliknya, jika puncaknya tersebar merata, berarti tinggi badan siswa terdistribusi secara lebih merata.

Perbedaan Histogram dengan Grafik Lain

Pemahaman tentang perbedaan antara histogram dan grafik lain sangat penting dalam analisis data. Kemampuan untuk memilih grafik yang tepat dapat memberikan gambaran yang lebih jelas dan akurat tentang distribusi data.

Perbedaan Histogram dengan Grafik Batang

Meskipun keduanya menampilkan data kategorikal, histogram dan grafik batang memiliki perbedaan mendasar. Histogram digunakan untuk data numerik yang berkelanjutan, menampilkan distribusi frekuensi, sedangkan grafik batang digunakan untuk membandingkan kategori diskrit. Histogram menampilkan rentang nilai, sedangkan grafik batang menampilkan nilai pada titik-titik tertentu.

Histogram menggambarkan distribusi frekuensi, sedangkan grafik batang membandingkan kategori.
Histogram berfokus pada rentang nilai, sedangkan grafik batang berfokus pada nilai spesifik pada masing-masing kategori.
Pada histogram, area batang mewakili frekuensi, sedangkan pada grafik batang, tinggi batang mewakili nilai.

Perbedaan Histogram dengan Grafik Garis

Grafik garis digunakan untuk menampilkan tren atau perubahan data dari waktu ke waktu, atau hubungan antara dua variabel. Histogram, di sisi lain, berfokus pada distribusi frekuensi data. Grafik garis lebih cocok untuk data yang berubah secara kontinu, sedangkan histogram untuk data yang terkelompok dalam rentang.

Grafik garis menunjukkan tren atau pola dalam data, sementara histogram menampilkan distribusi frekuensi.
Grafik garis cocok untuk data yang kontinu, sedangkan histogram untuk data yang terkelompok.
Grafik garis biasanya menunjukkan hubungan antara dua variabel, sedangkan histogram hanya menunjukkan distribusi satu variabel.

Perbandingan Histogram dengan Grafik Lain

Grafik	Jenis Data	Tujuan	Representasi	Interpretasi
Histogram	Numerik, berkelanjutan	Menunjukkan distribusi frekuensi	Batang berdampingan, area mewakili frekuensi	Melihat pola distribusi, misalnya simetris, miring, atau bimodal
Grafik Batang	Kategorikal, diskrit	Membandingkan kategori	Batang terpisah, tinggi mewakili nilai	Membandingkan nilai pada setiap kategori
Grafik Garis	Numerik, kontinu (sering berasosiasi dengan waktu)	Menunjukkan tren atau pola	Garis yang menghubungkan titik-titik data	Melihat perubahan atau kecenderungan data dari waktu ke waktu

Pengaruh Karakteristik Data

Karakteristik data, seperti jenis data (diskrit atau kontinu), rentang nilai, dan jumlah data, sangat memengaruhi pilihan grafik yang tepat. Data yang berkelanjutan dan memiliki rentang nilai yang luas akan lebih cocok divisualisasikan menggunakan histogram.

Contoh Perbedaan Visual

Bayangkan data tentang tinggi badan siswa. Jika menggunakan grafik batang, kita akan membandingkan jumlah siswa dalam setiap kategori tinggi badan (misalnya, 150-155 cm, 155-160 cm, dst). Jika menggunakan histogram, kita akan melihat distribusi tinggi badan secara keseluruhan, dengan setiap batang mewakili rentang tinggi badan tertentu dan luasnya mewakili frekuensi siswa dalam rentang tersebut. Histogram akan memberikan gambaran yang lebih komprehensif tentang distribusi tinggi badan siswa dibandingkan grafik batang.

Permasalahan dan Solusi pada Histogram

Histogram, sebagai alat visualisasi data, seringkali menghadapi permasalahan dalam pembuatan dan interpretasinya. Pemahaman mendalam tentang potensi permasalahan dan solusi yang tepat sangat krusial untuk menghasilkan interpretasi yang akurat dan menghindari kesimpulan yang salah.

Potensi Permasalahan dalam Pembuatan Histogram

Beberapa potensi permasalahan yang dapat muncul dalam pembuatan histogram meliputi pemilihan rentang kelas yang tidak tepat, jumlah kelas yang terlalu sedikit atau terlalu banyak, dan representasi visual yang kurang efektif. Hal ini dapat mengakibatkan distorsi informasi dan interpretasi yang salah.

Rentang Kelas yang Tidak Tepat: Rentang kelas yang terlalu sempit atau terlalu lebar dapat memberikan gambaran yang tidak akurat tentang distribusi data. Rentang kelas yang terlalu sempit dapat menghasilkan histogram yang terlalu padat, sementara rentang kelas yang terlalu lebar dapat mengaburkan pola distribusi data.
Jumlah Kelas yang Tidak Tepat: Jumlah kelas yang terlalu sedikit dapat mengaburkan pola distribusi data, sedangkan jumlah kelas yang terlalu banyak dapat membuat histogram terlihat terlalu kompleks dan sulit diinterpretasikan. Pemilihan jumlah kelas yang tepat sangat penting untuk mendapatkan representasi visual yang baik.
Representasi Visual yang Kurang Efektif: Ketidakjelasan pada sumbu-sumbu (sumbu horizontal dan vertikal) atau judul yang tidak informatif dapat membuat histogram sulit dipahami. Penampilan histogram yang kurang menarik dapat membuat interpretasi menjadi kurang efektif.

Solusi untuk Mengatasi Permasalahan dalam Pembuatan Histogram

Untuk mengatasi permasalahan-permasalahan tersebut, beberapa langkah dapat dilakukan, seperti:

Memilih Rentang Kelas yang Tepat: Rentang kelas yang ideal harus mempertimbangkan rentang data yang ada dan jumlah data yang dimiliki. Rentang kelas yang terlalu lebar atau sempit perlu dipertimbangkan ulang.
Menentukan Jumlah Kelas yang Optimal: Jumlah kelas yang tepat dapat ditentukan dengan menggunakan aturan Sturges atau metode lain yang sesuai. Pemilihan yang tepat akan memberikan visualisasi yang optimal.
Membuat Representasi Visual yang Jelas: Pastikan sumbu horizontal dan vertikal memiliki label yang jelas dan informatif. Judul histogram harus menggambarkan data yang ditampilkan. Gunakan warna dan desain yang sesuai untuk meningkatkan pemahaman visual.

Contoh Permasalahan dan Solusinya

Bayangkan data nilai ujian matematika 30 siswa. Jika rentang nilai terlalu lebar (misalnya, 0-100), akan sulit untuk melihat distribusi frekuensi. Solusi: Menggunakan rentang kelas yang lebih spesifik (misalnya, 50-60, 60-70, dan seterusnya).

Mengatasi Data yang Tidak Terdistribusi Normal

Data yang tidak terdistribusi normal dapat menghasilkan histogram yang tidak simetris atau memiliki bentuk yang tidak biasa. Hal ini dapat membuat interpretasi menjadi lebih kompleks. Namun, dengan pendekatan yang tepat, distribusi data yang tidak normal dapat divisualisasikan dengan jelas dan informatif.

Menerapkan Transformasi Data: Transformasi data, seperti logaritma atau akar kuadrat, dapat digunakan untuk mengubah distribusi data menjadi lebih normal, sehingga histogram lebih mudah diinterpretasikan.
Menggunakan Histogram dengan Kelas yang Lebih Banyak: Menggunakan lebih banyak kelas dapat membantu menunjukkan bentuk distribusi yang tidak normal secara lebih rinci.
Menekankan Informasi Kritis: Fokus pada informasi yang penting dalam data yang tidak terdistribusi normal, seperti nilai minimum, maksimum, dan kuartil.

Mengatasi Kesalahan Umum dalam Interpretasi Histogram

Kesalahan umum dalam menginterpretasikan histogram antara lain mengabaikan konteks data, menyamakan frekuensi dengan nilai, dan tidak mempertimbangkan rentang kelas. Penting untuk memahami konteks data dan makna dari setiap nilai pada sumbu-sumbu.

Simpulan Akhir

Kesimpulannya, histogram merupakan alat visualisasi data yang sangat penting dalam matematika. Dengan pemahaman yang baik tentang komponen, cara pembuatan, dan interpretasinya, histogram dapat membantu kita dalam menganalisis data, mengidentifikasi pola, dan membuat keputusan yang lebih baik. Semoga artikel ini memberikan pemahaman yang komprehensif dan bermanfaat tentang materi matematika histogram.